What Is 330 Degrees In Radians

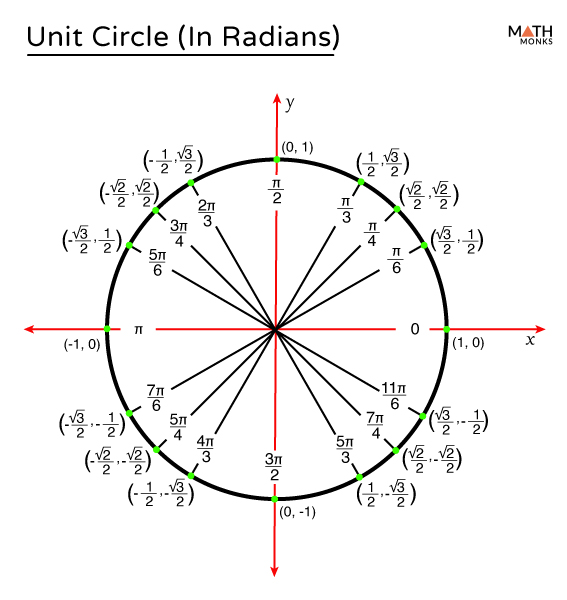
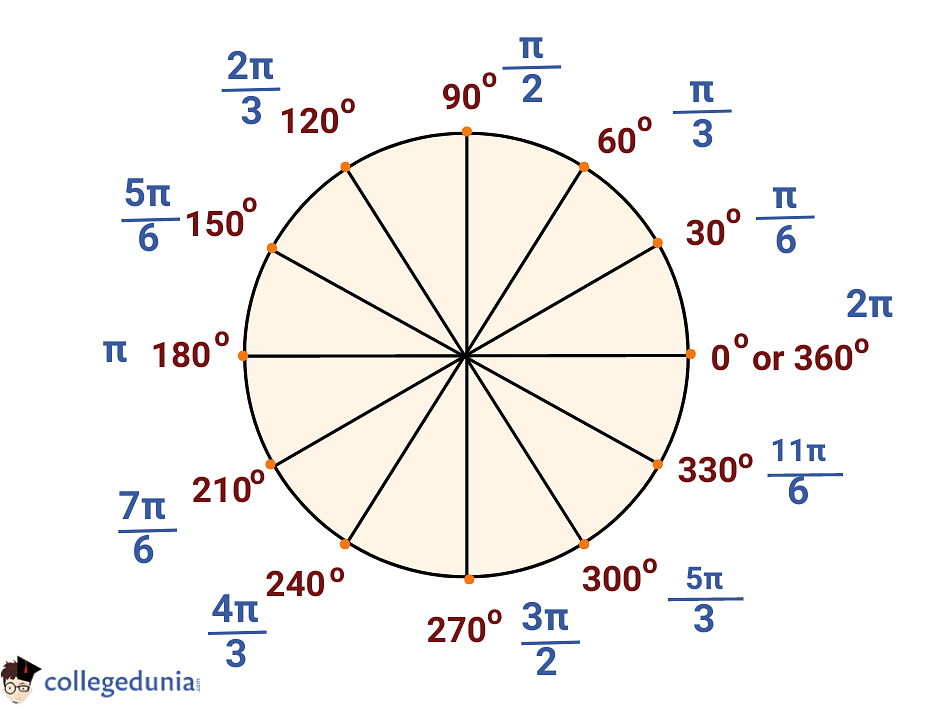
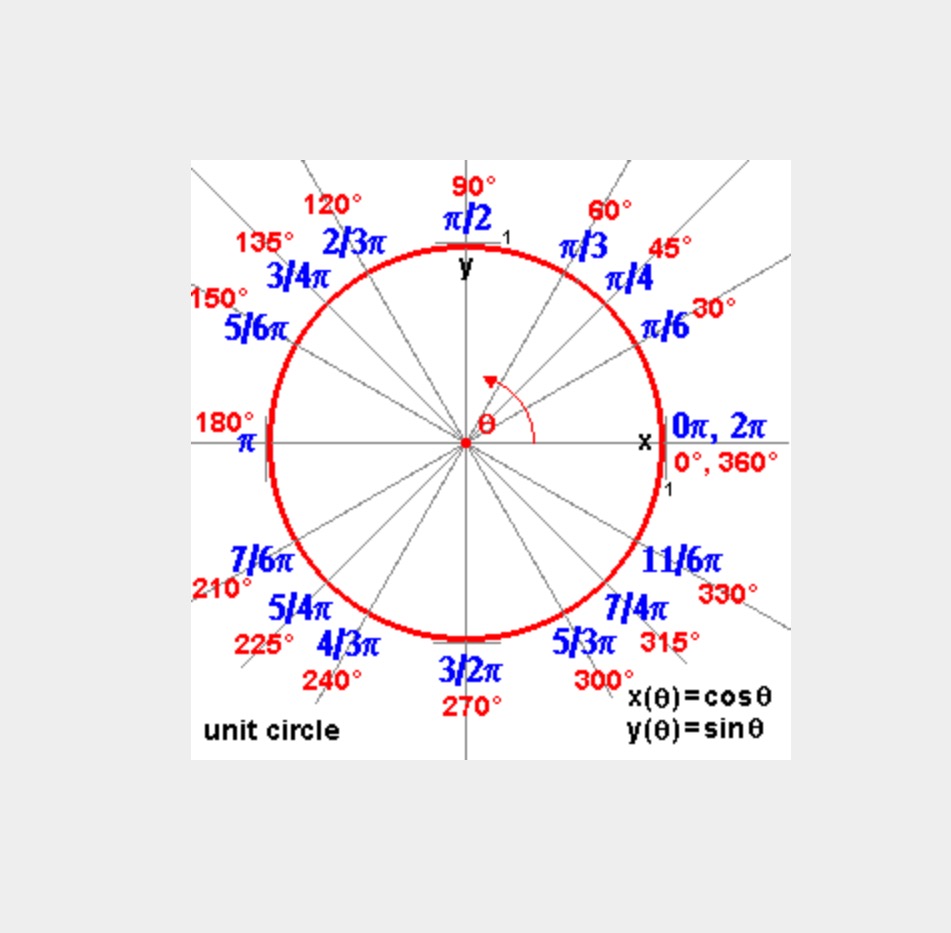
What Is 330 Degrees In Radians - 330 degrees is equal to 11π / 6 radians. Since pi radians are equal. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. To convert 330 degrees to radians, we can use the conversion formula: 330 degrees is equal to 11π/6 radians. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. What is 330 degrees in radians? 11π/6 rad can be expressed as real. Cancel the common factor of 30 30. 11π/6 radians, when reduced to lowest fraction in terms of π.

Cancel the common factor of 30 30. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. 330 degrees is equal to 11π / 6 radians. What is 330 degrees in radians? To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. 11π/6 radians, when reduced to lowest fraction in terms of π. 330 degrees is equal to 11π/6 radians. 11π/6 rad can be expressed as real. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians.

330 degrees is equal to 11π / 6 radians. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. Since pi radians are equal. 11π/6 rad can be expressed as real. 11π/6 radians, when reduced to lowest fraction in terms of π. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. Cancel the common factor of 30 30. Cancel the common factor of 30 30. To convert 330 degrees to radians, we can use the conversion formula: 330 degrees is equal to 11π/6 radians.

Radian Conversion Chart

To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. 11π/6 radians, when reduced to lowest fraction in terms of π. To convert 330 degrees to radians, we can use the conversion formula: Cancel the common factor of 30 30. What is 330 degrees in radians?

Comment convertir des degrés en radians 5 étapes

To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. Cancel the common factor of 30 30. To convert 330 degrees to radians, we can use the.

Unit Circle Radians Chart

To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. Cancel the common factor of 30 30. To convert 330 degrees to radians, we can use the conversion formula: 11π/6 radians, when reduced to lowest fraction in terms of π. To convert degrees to radians, multiply by π 180° π 180 °,.

Find the Exact Value of the Tangent of 330 Degrees Using the Unit

330 degrees is equal to 11π / 6 radians. To convert 330 degrees to radians, we can use the conversion formula: To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. To convert degrees to radians, we use the fact that 1 revolution is 360.

Unit 7 More Geometry

To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. To convert 330 degrees to radians, we can use the conversion formula: Since pi radians are equal. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula..

FileDegreeRadian Wikipedia, 48 OFF

330 degrees is equal to 11π / 6 radians. To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. 11π/6 rad can be expressed as real. To.

Relation Between Degree and Radian Conversion and Examples

Since pi radians are equal. What is 330 degrees in radians? To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. 11π/6 rad can be expressed as real. To convert 330 degrees to radians, we can use the conversion formula:

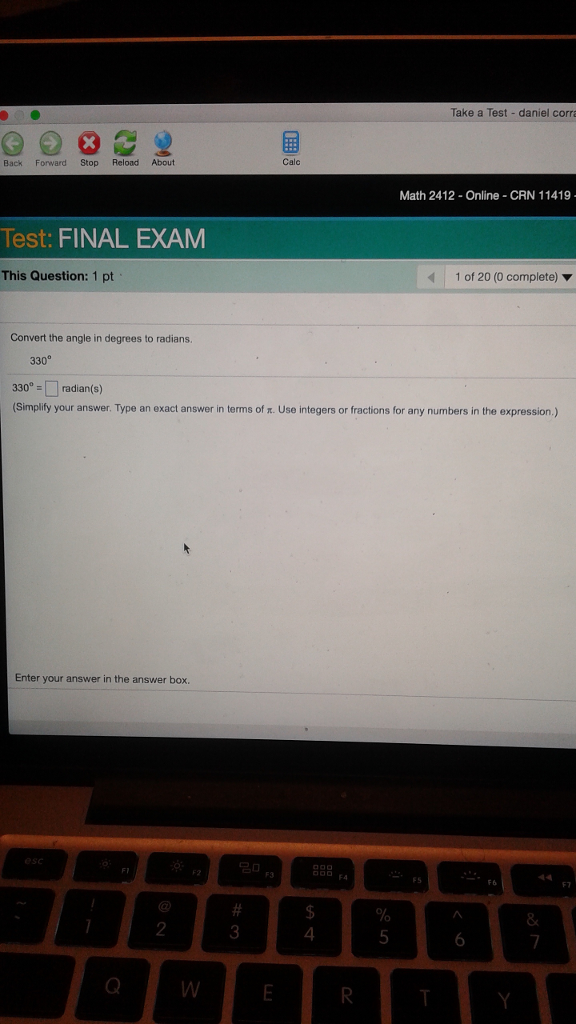
Solved Convert the angle in degrees to radians. 330 degree

To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. Since pi radians are equal. Cancel the common factor of 30 30. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. What is 330 degrees in radians?

How Many Radians Is Pi

What is 330 degrees in radians? To convert 330 degrees to radians, we can use the conversion formula: Cancel the common factor of 30 30. To convert degrees to radians, we use the fact that 1 revolution is 360 degrees, which is. 11π/6 rad can be expressed as real.

File30 degree rotations expressed in radian measure.svg Math methods

To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. To convert 330 degrees to radians, we can use the conversion formula: To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. 11π/6 radians, when reduced to.

11Π/6 Rad Can Be Expressed As Real.

11π/6 radians, when reduced to lowest fraction in terms of π. What is 330 degrees in radians? To convert a measurement in degrees to a measurement in radians, you need to use a conversion formula. Cancel the common factor of 30 30.

To Convert Degrees To Radians, Multiply By Π 180° Π 180 °, Since A Full Circle Is 360° 360 ° Or 2Π 2 Π Radians.

To convert 330 degrees to radians, we can use the conversion formula: 330 degrees is equal to 11π/6 radians. To convert degrees to radians, multiply by π 180° π 180 °, since a full circle is 360° 360 ° or 2π 2 π radians. 330 degrees is equal to 11π / 6 radians.