Surface Area And Volume Relationship
Surface Area And Volume Relationship - The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. How to calculate surface area to volume ratio? First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
How to calculate surface area to volume ratio? The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
How to calculate surface area to volume ratio? The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
(a) Water depthVolume relationship and (b) water surface areavolume
The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. First, calculate the surface area (sa) of the object using the appropriate formula for its shape. How to calculate surface area to volume ratio?
Surface Area & Volume Combination of Solids EuroSchool
The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. How to calculate surface area to volume ratio? First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
Surface Area_Volume Relationship PDF Cell (Biology) Cell Membrane
How to calculate surface area to volume ratio? First, calculate the surface area (sa) of the object using the appropriate formula for its shape. The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of.
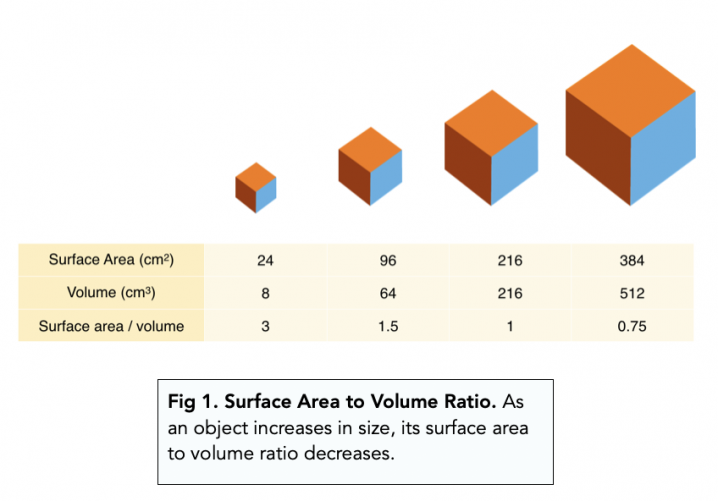
Relationship between surface area and volume changes as a function of size
First, calculate the surface area (sa) of the object using the appropriate formula for its shape. The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. How to calculate surface area to volume ratio?
Understanding Surface Area to Volume Ratio (Alevel Biology) Study Mind
How to calculate surface area to volume ratio? The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
Surface Area to Volume Ratio YouTube
How to calculate surface area to volume ratio? The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
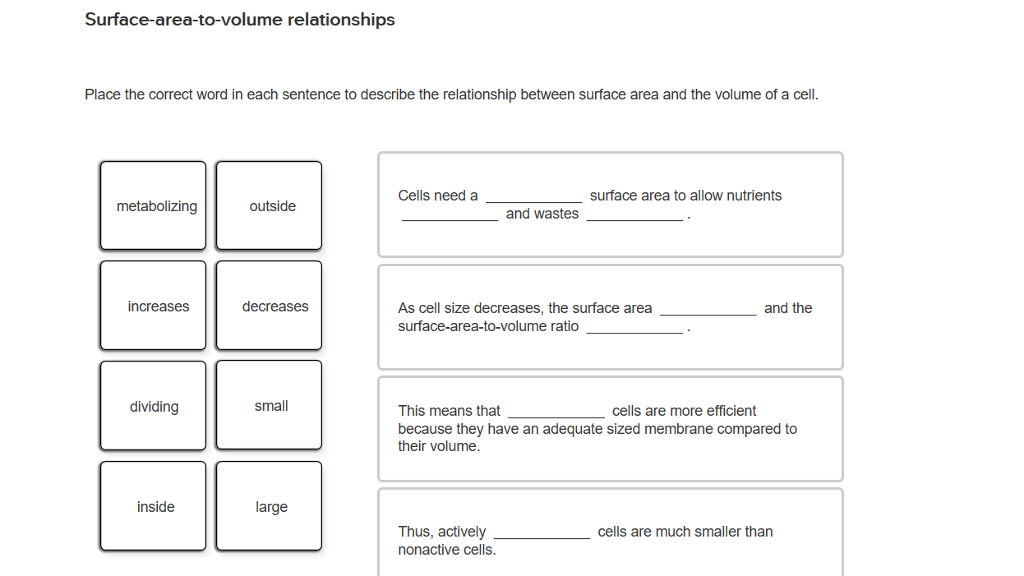
Solved Surfaceareatovolume relationships Place the
How to calculate surface area to volume ratio? The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
How to Calculate Surface Area to Volume Ratio GCSE Biology
First, calculate the surface area (sa) of the object using the appropriate formula for its shape. How to calculate surface area to volume ratio? The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of.
(a) Water depthVolume relationship and (b) water surface areavolume
First, calculate the surface area (sa) of the object using the appropriate formula for its shape. How to calculate surface area to volume ratio? The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of.
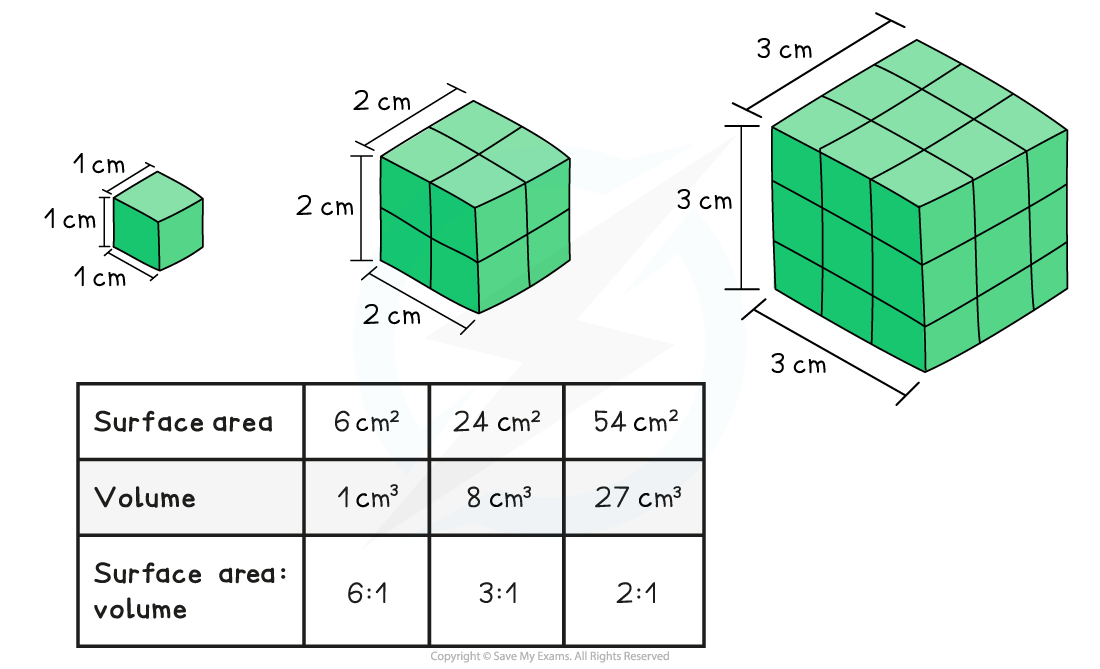
CIE A Level Biology复习笔记4.2.7 Surface Area to Volume Ratios翰林国际教育
The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. How to calculate surface area to volume ratio? First, calculate the surface area (sa) of the object using the appropriate formula for its shape.
First, Calculate The Surface Area (Sa) Of The Object Using The Appropriate Formula For Its Shape.
The ball has volume $v(r) = \frac{4}{3}\pi r^3$, where $r$ is the radial distance from the origin to the boundary $\partial b$ of. How to calculate surface area to volume ratio?