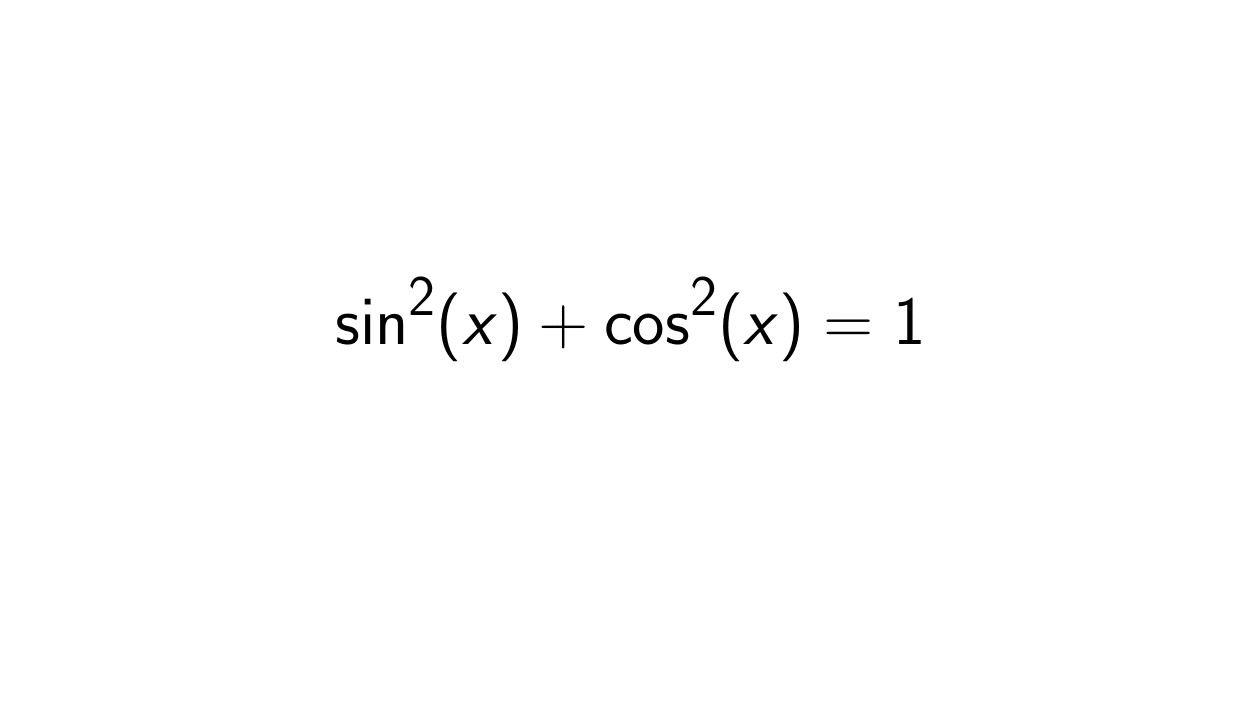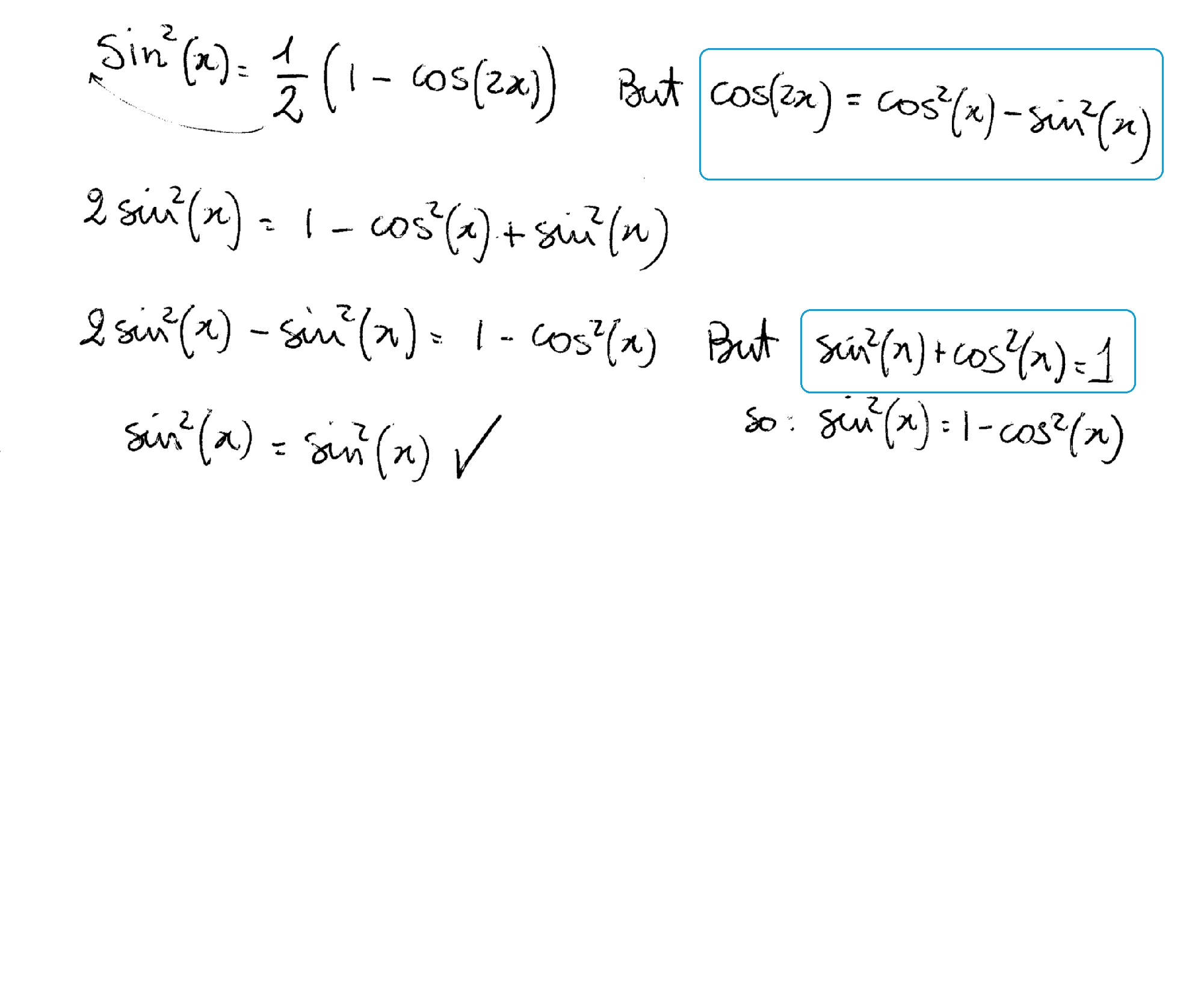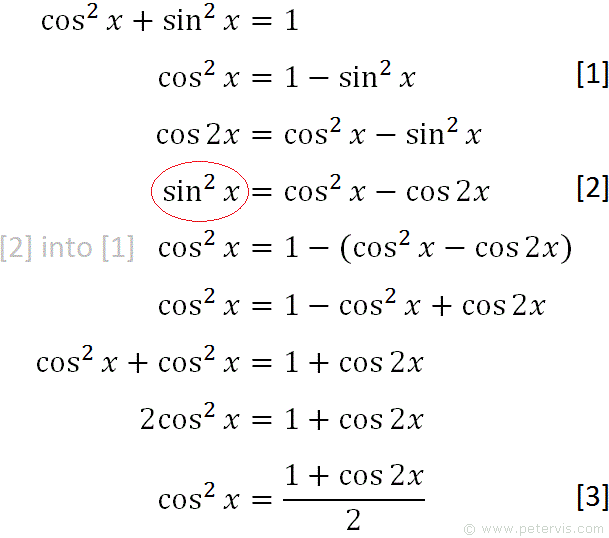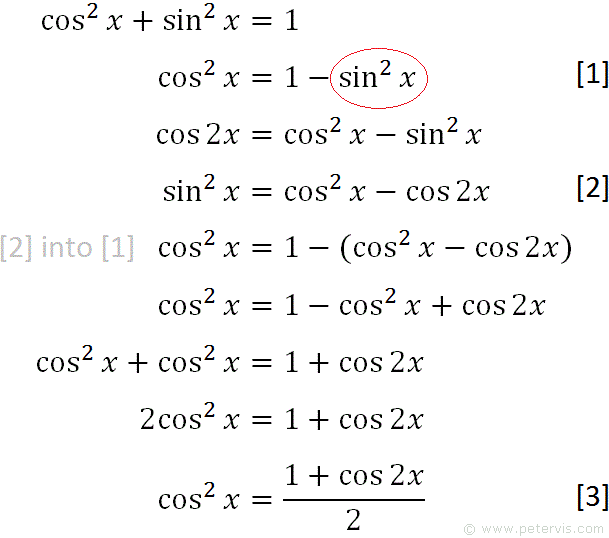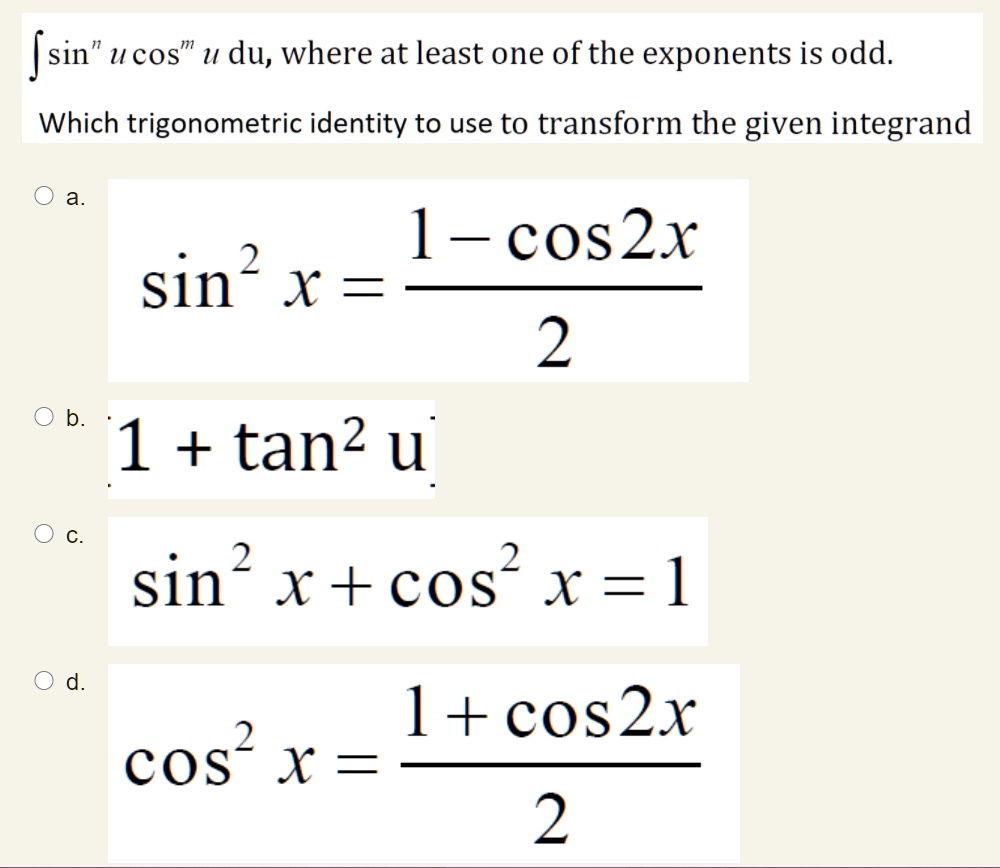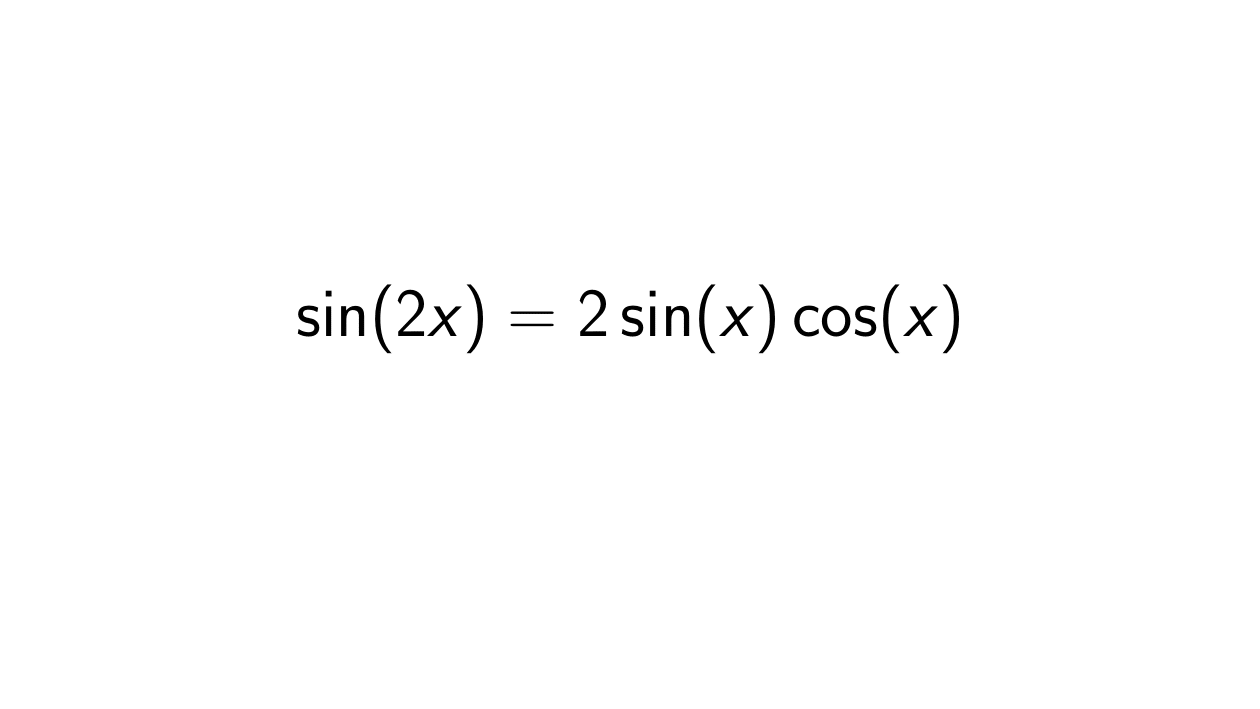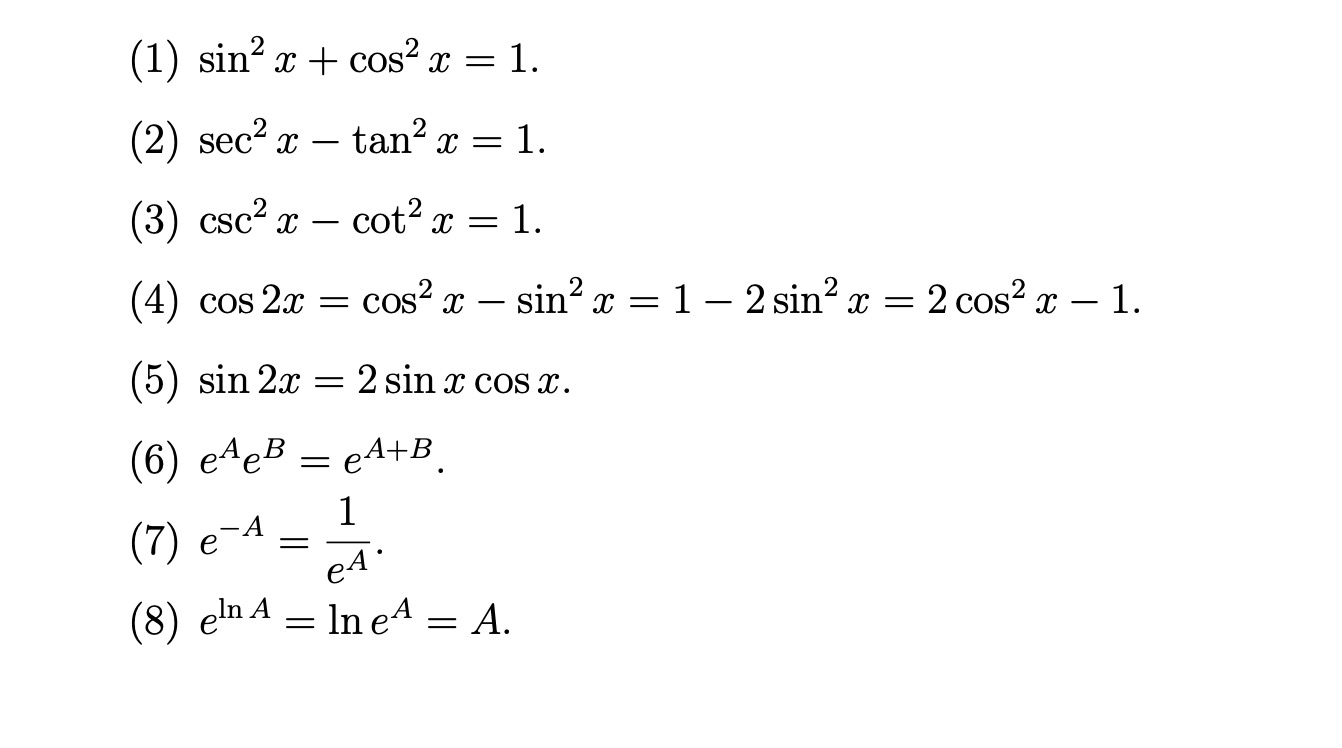Sin 2 Cos 2 1
Sin 2 Cos 2 1 - Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: Sin2x +cos2x = 1 ⇒. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values.
Sin2x +cos2x = 1 ⇒. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs.
Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Sin2x +cos2x = 1 ⇒. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally.
sin^2(x) + cos^2(x) = 1 Trig Identity Graphical Proof YouTube
Sin2x +cos2x = 1 ⇒. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. The most fundamental of all trigonometric.
Prove that sin^2(x) + cos^2(x) = 1 Epsilonify
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the.
How do you verify sin^2(x) = (1/2)(1cos2x)? Socratic
The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Just as the distance between the origin and any point (x,y) on a circle must be the circle's.
Solved Explain what's wrong with this proof since cos^2
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: Just as the distance between the origin and any point (x,y) on a circle must be.
Ex 5.6, 5 Find dy/dx, x = cos cos 2, y = sin sin 2
The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of.
Cos 2 Sin 2 Identity on Sale
Sin2x +cos2x = 1 ⇒. It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Just as the distance between the origin and any point (x,y) on a.
Sine Formula Triangle
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. Sin2x +cos2x = 1 ⇒. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. The most fundamental of all trigonometric.
SOLVED Sin U Cos U Du, Where At Least One Of The Exponents, 48 OFF
The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Sin2x +cos2x = 1 ⇒. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. It so happens that #sin^2(x) + cos^2(x) = 1# is one of.
Prove that sin(2x) = 2sin(x)cos(x) Epsilonify
It so happens that #sin^2(x) + cos^2(x) = 1# is one of the easier identities to prove using other methods, and so is generally. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the.
Here is a list of identities involving trigonometric
Sin2x +cos2x = 1 ⇒. Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Replace in the equation cos2x by (1 − sin2x) we know this.
It So Happens That #Sin^2(X) + Cos^2(X) = 1# Is One Of The Easier Identities To Prove Using Other Methods, And So Is Generally.
Just as the distance between the origin and any point (x,y) on a circle must be the circle's radius, the sum of the squared values. Replace in the equation cos2x by (1 − sin2x) we know this is true through manipulation of the pythagorean identity: The most fundamental of all trigonometric identities 'sin^2(x) + cos^2(x) = 1', a basis of many other proofs. Sin2x +cos2x = 1 ⇒.