Faraday S Law Integral Form
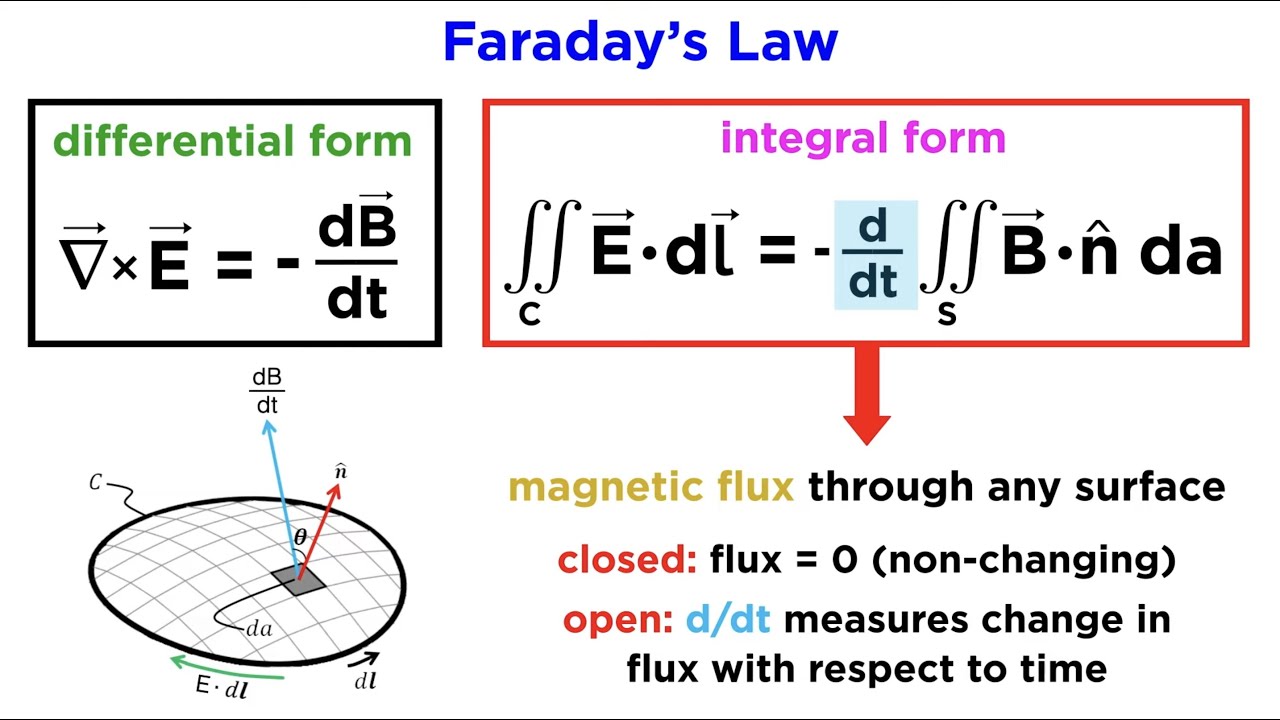
Faraday S Law Integral Form - Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction may be stated as follows: Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. The induced emf ε in a coil is proportional to the negative of the rate of change of. I want to understand how stoke's theorem shows that the integral form of faraday's law:
Faraday’s law of induction may be stated as follows: Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. The induced emf ε in a coil is proportional to the negative of the rate of change of. Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric.
The induced emf ε in a coil is proportional to the negative of the rate of change of. Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction may be stated as follows:
Electrical and Electronics Engineering Faraday's Law
Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. I want to understand how stoke's theorem shows that the integral form of faraday's law: Let's consider both the integral and.
Maxwell’s Equations Part 3 Faraday’s Law YouTube
Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): The induced emf ε in a coil is proportional to the negative of the rate of change of. Using stokes’ theorem, this.
Faraday's Law Understanding the Alternative (Integral Form)
Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. I want to understand how stoke's theorem shows that the integral form of faraday's law: The induced emf ε in a coil is proportional to the.
General form of Faraday’s Law
The induced emf ε in a coil is proportional to the negative of the rate of change of. I want to understand how stoke's theorem shows that the integral form of faraday's law: Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Let's consider both the integral and differential equations which.
Solved Derive the differential form of Faraday's law of
Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday’s law of induction is.
Faraday's Law Calculations
Faraday’s law of induction may be stated as follows: I want to understand how stoke's theorem shows that the integral form of faraday's law: Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an.
PPT Faraday’s Law PowerPoint Presentation, free download ID3607741
I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies. The induced emf ε in a coil is proportional to the negative of the rate of change of. Let's consider both the integral.
Solved Maxwell's Equations in a Medium Equations Integral
Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): I want to understand how stoke's theorem shows that the integral form of faraday's law: Faraday’s law of induction may be stated as follows: Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material,.
Faraday Law, standard (integral form) Physics and mathematics
Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Faraday's law of induction explains.
Field Integral Equation Derivation Tessshebaylo
Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric. The induced emf ε in a coil is proportional to the negative of the rate of change of. Using stokes’ theorem, this law.
I Want To Understand How Stoke's Theorem Shows That The Integral Form Of Faraday's Law:
Faraday’s law of induction may be stated as follows: Let's consider both the integral and differential equations which express the faraday law (3rd maxwell equation): Using stokes’ theorem, this law can be written in integral form as \begin {equation} \label {eq:ii:17:2} \oint_\gamma\flpe\cdot d\flps=. Faraday's law of induction explains that a changing magnetic flux can induce a current in a loop of conducting material, and quantifies.
The Induced Emf Ε In A Coil Is Proportional To The Negative Of The Rate Of Change Of.
Faraday’s law of induction is a basic law of electromagnetism that predicts how a magnetic field will interact with an electric.