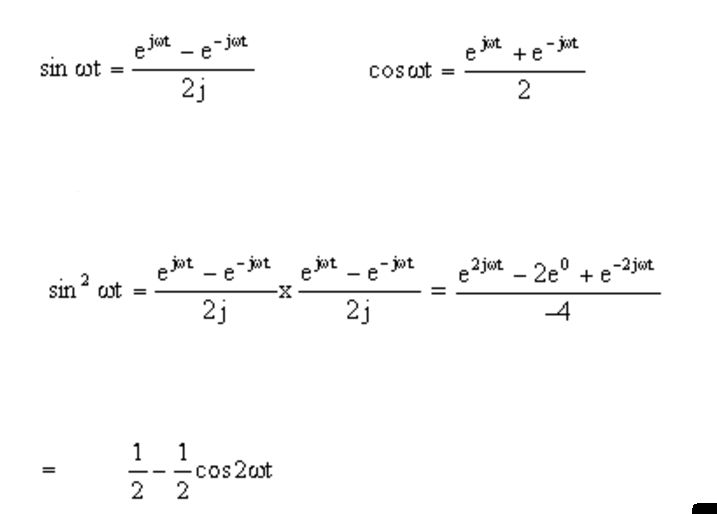
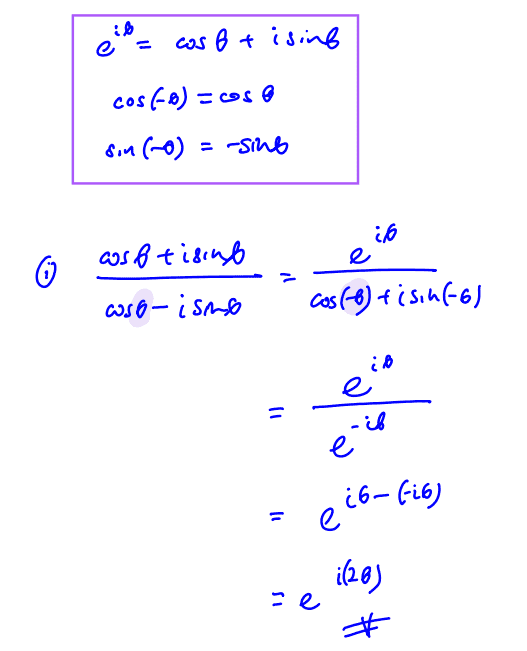Cos Exponential Form
Cos Exponential Form - In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that.
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions:
In euler's formula, if we. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that.
Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers.
Expressing Various Complex Numbers in Exponential Form Tim Gan Math
According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: In.
Question Video Converting the Product of Complex Numbers in Polar Form
According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers.
Basics of QPSK modulation and display of QPSK signals Electrical
In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t.
Exponential Form of Complex Numbers
From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: In euler's formula, if we. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t.
Expressing Various Complex Numbers in Exponential Form Tim Gan Math
According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers.
Question Video Converting Complex Numbers from Polar to Exponential
In euler's formula, if we. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: From these relations and the properties of exponential multiplication you can painlessly prove all sorts.
A Trigonometric Exponential Equation with Sine and Cosine Math
In euler's formula, if we. From these relations and the properties of exponential multiplication you can painlessly prove all sorts of trigonometric identities that. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t.
Euler's exponential values of Sine and Cosine Exponential values of
In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. From these relations and the properties of exponential multiplication you can painlessly prove all sorts.
part 1 _exponential form of a complex form YouTube
According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. In euler's formula, if we. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: From these relations and the properties of exponential multiplication you can painlessly prove all sorts.
From These Relations And The Properties Of Exponential Multiplication You Can Painlessly Prove All Sorts Of Trigonometric Identities That.
In euler's formula, if we. According to euler, we should regard the complex exponential eit as related to the trigonometric functions cos( t ) and sin( t ) via the following. Euler's formula is a relationship between exponents of imaginary numbers and the trigonometric functions: