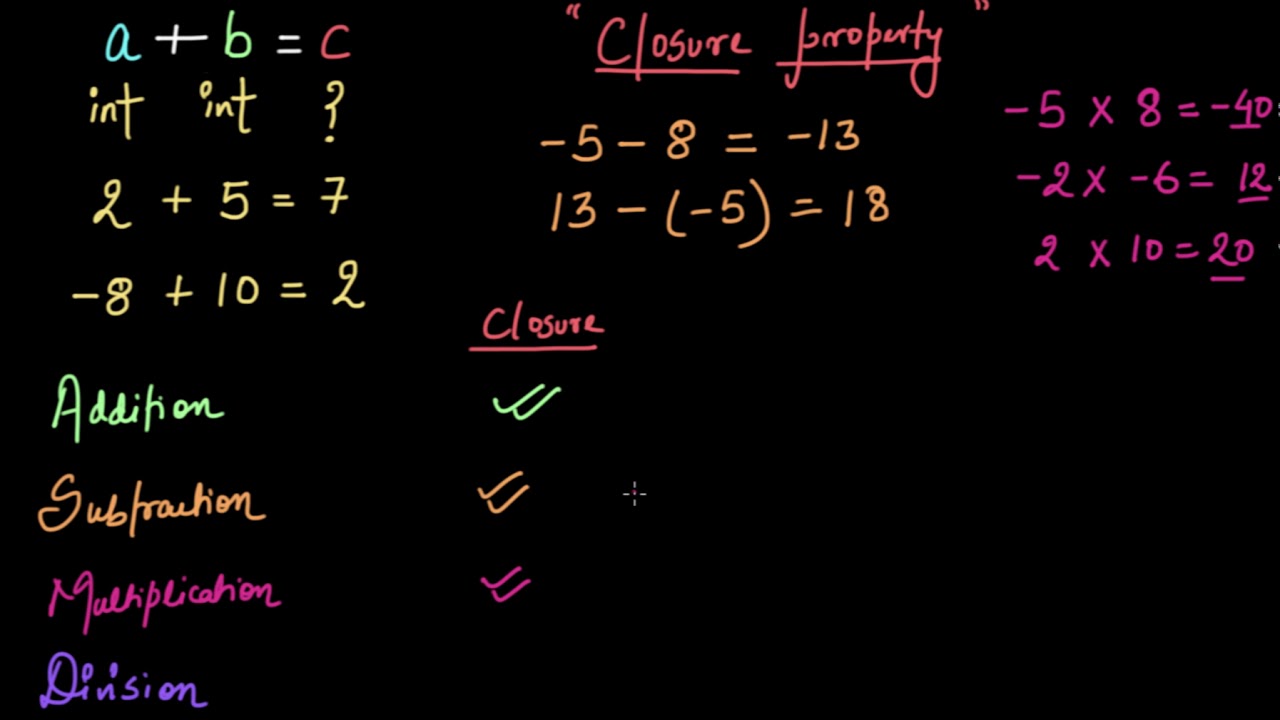Closure Math Property
Closure Math Property - Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. Closure property holds for addition and multiplication of whole numbers. A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure property of whole numbers under addition:
A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure property holds for addition and multiplication of whole numbers. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. Closure property of whole numbers under addition:
A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. Closure property of whole numbers under addition: Closure property holds for addition and multiplication of whole numbers.
Closure Property Of Addition Definition slidesharetrick
Closure property holds for addition and multiplication of whole numbers. A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the.
Properties of Integers Closure Property MathsMD
A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. Closure property holds for addition and multiplication of.
Whole Numbers(Part1) Closure Property of Whole Numbers MathsGrade7
A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. Closure property of whole numbers under addition: Closure.
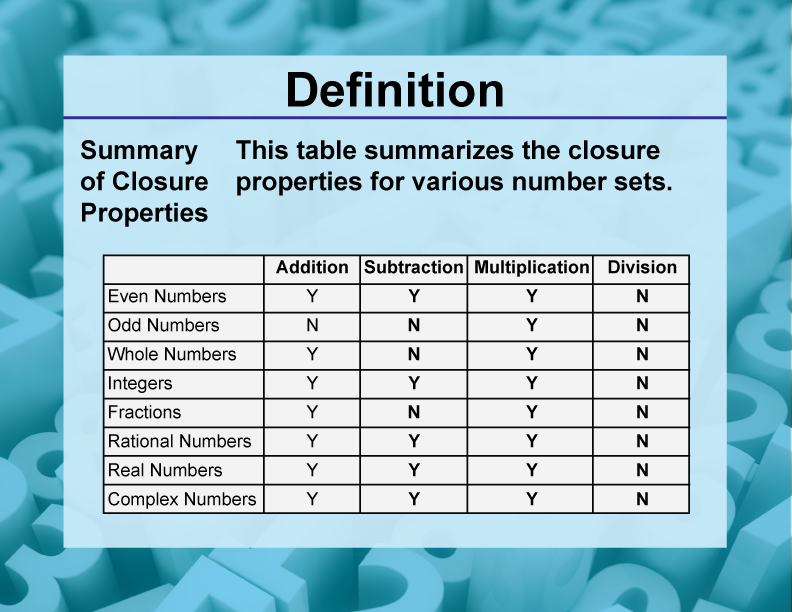
DefinitionClosure Property TopicsSummary of Closure Properties
Closure property of whole numbers under addition: Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure.
Integers closure property of multiplication YouTube
Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. Closure property of whole numbers under addition: Closure property holds for addition and multiplication of whole numbers. A set is closed (under an operation) if and only if the operation on any two elements of.
Algebra 1 2.01d The Closure Property YouTube
Closure property of whole numbers under addition: Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure.
DefinitionClosure Property TopicsEven Numbers and Closure Addition
Closure property holds for addition and multiplication of whole numbers. Closure property of whole numbers under addition: Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed (under an operation) if and only if the operation on any two elements of.
Math Definitions Collection Closure Properties Media4Math
Closure property of whole numbers under addition: Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure.
04 Proving Closure Property For Rational numbers YouTube
Closure property holds for addition and multiplication of whole numbers. Closure is when an operation (such as adding) on members of a set (such as real numbers) always makes a member of the same set. A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the.
What Is Closure Property Definition, Formula, Examples
A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure property holds for addition and multiplication of whole numbers. Closure property of whole numbers under addition: Closure is when an operation (such as adding) on members of a set (such as real.
Closure Is When An Operation (Such As Adding) On Members Of A Set (Such As Real Numbers) Always Makes A Member Of The Same Set.
Closure property holds for addition and multiplication of whole numbers. A set is closed (under an operation) if and only if the operation on any two elements of the set produces another element of the same set. Closure property of whole numbers under addition: